Why the PHL is one of the best rocket launch sites in the world

Our country's location near the equator makes us a prime candidate for being the go-to rocket launch site for all the world's  space agencies—a big ace up our sleeves, given our own nascent space program.

Yes, it's possible to design increasingly powerful rockets to cope with ever-bigger payload demands, but the cost of designing and rolling out new rockets is a slow and expensive process.

However, we can take advantage of the very Earth itself to send rockets into orbit: it's all a matter of finding the right location—and the Philippines is a very choice spot for this.

How so?

The secret is in how the Earth affects a rocket before and after it's launched.

Rocket at rest: more than meets the eye

It might seem that a rocket has zero initial velocity while sitting idly on its launch pad. However, since that launch pad is also sitting on a spinning Earth, the rocket is actually already moving about the Earth’s axis.

The farther away you are from the Earth's axis, the more tangential velocity is imparted onto a rocket.

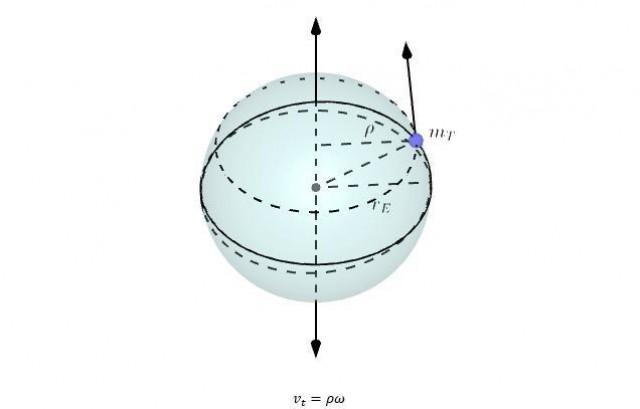
We can describe its movement depending on its latitude and distance from the Earth’s equator and axis:

In the above illustration, Φ is the latitude and R_E is the Earth’s radius, while ρ is the general distance from the axis of rotation. It’s easily seen that ρ is at its maximum at R_E.

Depending on what altitude the rocket sits, its velocity or tangential velocity will be:

In this equation, ω is the angular velocity, or how much it takes for a spinning object to complete a full spin. If you think about our planet as a big ball that takes 24 hours to complete a full spin,  ω would have a very small value, as we'll see in a bit.

Together with ρ, the tangential velocity vt is:

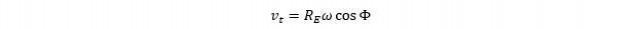
Now that we know how the rocket moves with respect to its latitude while resting on its launch pad, let’s look at how it moves as it reaches its designated altitude, from whence it will proceed to orbit.

Rocket at orbit: Orbital velocity

Now that our rocket has launched, consumed its fuel, and entered (in this case) a circular orbit, it now experiences centripetal force. This is the force responsible for making the rocket move in a circle around the Earth, free from its previous attachment to its launch pad.

This centripetal force also happens to be equivalent to the force of gravity, so we can represent this as:

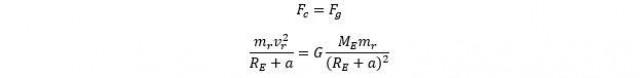
In the above equation, mr is the rocket’s mass after it has consumed its fuel; a is the altitude of the rocket's orbit—hence the orbital radius is simply equal to the Earth’s radius plus a. The orbital velocity vr i is the velocity at R_E + a.

Solving for v_r, we get:

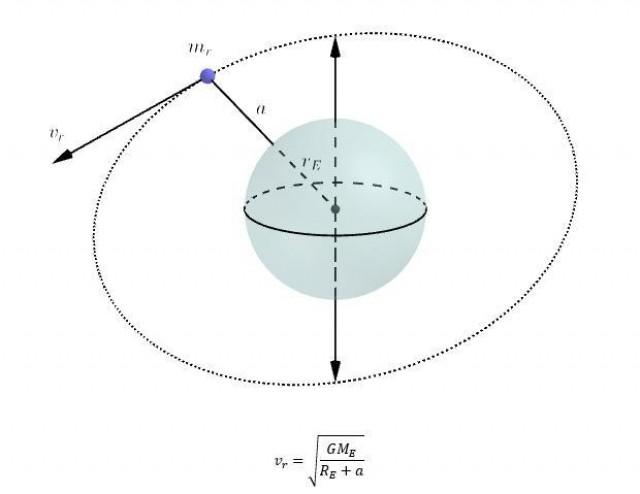
Now that we have the equations for initial and final velocity, delta v would simply be the difference between them.

But what use would that be? Enter the rocket equation.

The Rocket Equation

The “rocket equation” is:

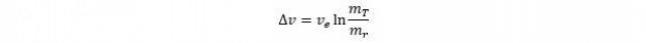
Where the change in velocity is written in shorthand as Δv; v_e is exhaust velocity, or the measure of the rocket's speed; m_T is the rocket’s mass with fuel; and m_r is the fuel-less mass of the rocket itself.

The exhaust velocity is also the product of the Earth’s acceleration due to gravity, g_o and the specific impulse of the rocket, I_sp, change in momentum per unit mass of fuel. Expanding the rocket equation using the previous equations leads to:

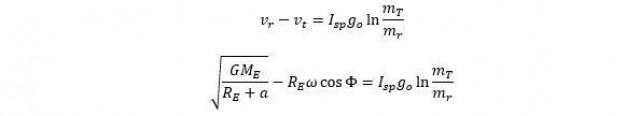
After simplifying this equation, solving for the fuel mass (m_f) leads to the expression of Φ as a function of m_f:

So let’s say we plan to launch a rocket similar to SpaceX’s much-publicized Falcon 9 v1.1, weighing 105,000kg without its first stage fuel and having a specific impulse of 280 s at sea level, to an altitude of 400km (a typical Low-Earth orbit) from a launch pad with a latitude of 30.0000°N (approximating Japan’s Tanegashima Space Center).

Now let's plug in these important values:

• radius of the Earth, R_E = 6,371,000 m
• gravitational constant, G = 6.674 x 10^-11
• mass of the Earth, M_E = 5.972 x 1024kg
• Earth’s angular velocity, ω = 7.292 x 10^-5 rad/s

So if we were to take off from Japan, the amount of first-stage fuel that would be burned would be 1,352,675.80kg.

But if we launch the rocket from a hypothetical launch pad from a point in Paulau, Sarangani, with the coordinates of 5.4431 °N, 128.4859 °E, the amount of fuel burned would only be 1,322,293.30kg.

That’s 30,382.49kg less fuel!

^{Palau, Saranggani. via Google Maps}

Furthermore, the minimum inclination of the orbit is equal to the latitude of the launch site. This means that launching from near the equator positions the rocket so that it needs to make minimal adjustments to its flight path, thereby consuming less fuel.

This is a very simplified example, to be sure, but it drives the point home.

How the PHL sizes up globally

Now let's look at a map of several actual launch sites around the world:

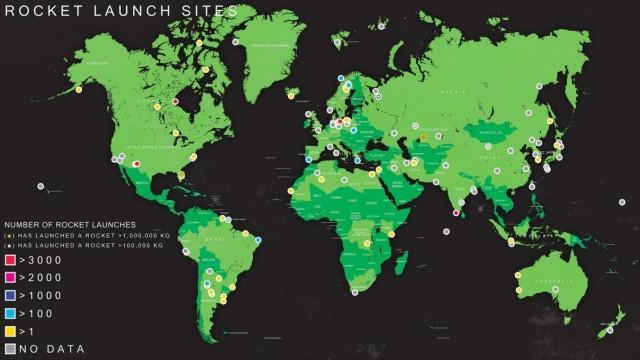
And here's how much fuel would be spent sending a rocket from each of these sites, all other things being equal:

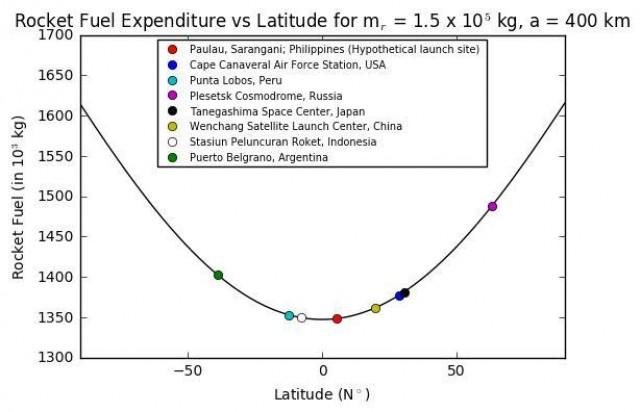
Note that launching from the Philippines gives you close to optimal savings.

Forward to the future

On a final note, as far as weather conditions are concerned, the southern Philippines' climate makes for evenly distributed rain and overall stable weather through the year.

With the dawn of the Philippine Space Agency, it's not too farfetched to dream of several local launch sites for us as well as for our international counterparts—and if private companies like SpaceX join the fray, why not?

Great times ahead, indeed. — TJD, GMA News

Lanz Anthonee Lagman is a BS Astronomy Technology student at Rizal Technological University and the current Editor-in-Chief of The Appulse, the official publication of the Philippine Astronomical Society. An earlier, expanded version of this essay appeared on The Mind Museum Blog.

References:
1. SpaceX Falcon 9 v1.1 Data Sheet. (2016, January 17)
2. Falcon 9 Launch Vehicle Payload User’s Guide (2015, October 21)
3. List of Rocket Launch Sites